GaussianCube: A Structured and Explicit Radiance Representation for 3D Generative Modeling

Bowen Zhang1, Yiji Cheng2, Jiaolong Yang3, Chunyu Wang3,
Feng Zhao1, Yansong Tang2, Dong Chen3, Baining Guo3.
1University of Science and Technology of China, 2Tsinghua University, 3Microsoft Research Asia
Paper Code

Abstract

We introduce a radiance representation that is both structured and fully explicit and thus greatly facilitates 3D generative modeling. Existing radiance representations either require an implicit feature decoder, which significantly degrades the modeling power of the representation, or are spatially unstructured, making them difficult to integrate with mainstream 3D diffusion methods. We derive GaussianCube by first using a novel densification-constrained Gaussian fitting algorithm, which yields high-accuracy fitting using a fixed number of free Gaussians, and then rearranging these Gaussians into a predefined voxel grid via Optimal Transport. Since GaussianCube is a structured grid representation, it allows us to use standard 3D U-Net as our backbone in diffusion modeling without elaborate designs. More importantly, the high-accuracy fitting of the Gaussians allows us to achieve a high-quality representation with orders of magnitude fewer parameters than previous structured representations for comparable quality, ranging from one to two orders of magnitude. The compactness of GaussianCube greatly eases the difficulty of 3D generative modeling. Extensive experiments conducted on unconditional and class-conditioned object generation, digital avatar creation, and text-to-3D synthesis all show that our model achieves state-of-the-art generation results both qualitatively and quantitatively, underscoring the potential of GaussianCube as a highly accurate and versatile radiance representation for 3D generative modeling.

Unconditional Generation Results

ShapeNet Car


ShapeNet Chair

Class-conditioned Generation Results

OmniObject3D

3D Digital Avatar Creation from Single Portrait Image

The portraits we used in this demo are either ai-generated or under free license. The 3D digital avatars generated by our model are for research purposes only.

Text-to-3D Synthesis

Method

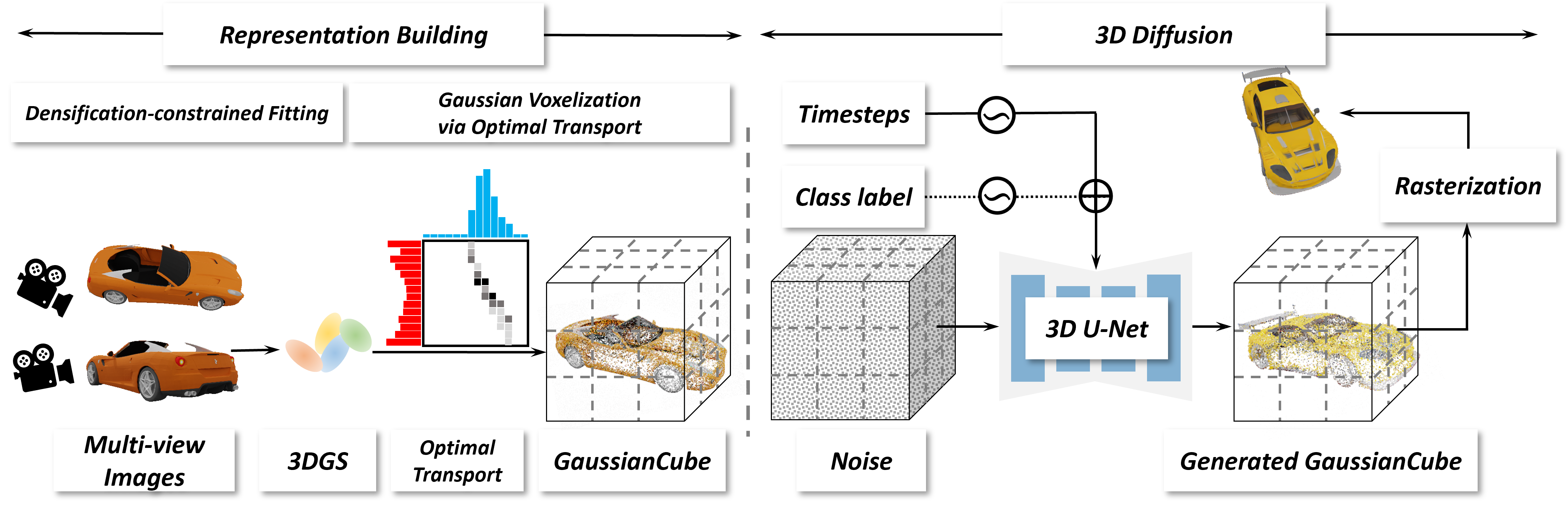
Our framework comprises two main stages of representation construction and 3D diffusion. In the representation construction stage, given multi-view renderings of a 3D asset, we perform densification-constrained fitting to obtain 3D Gaussians with constant numbers. Subsequently, the Gaussians are voxelized into GaussianCube via Optimal Transport. In the 3D diffusion stage, our 3D diffusion model is trained to generate GaussianCube from Gaussian noise.

Densification-constrained Fitting

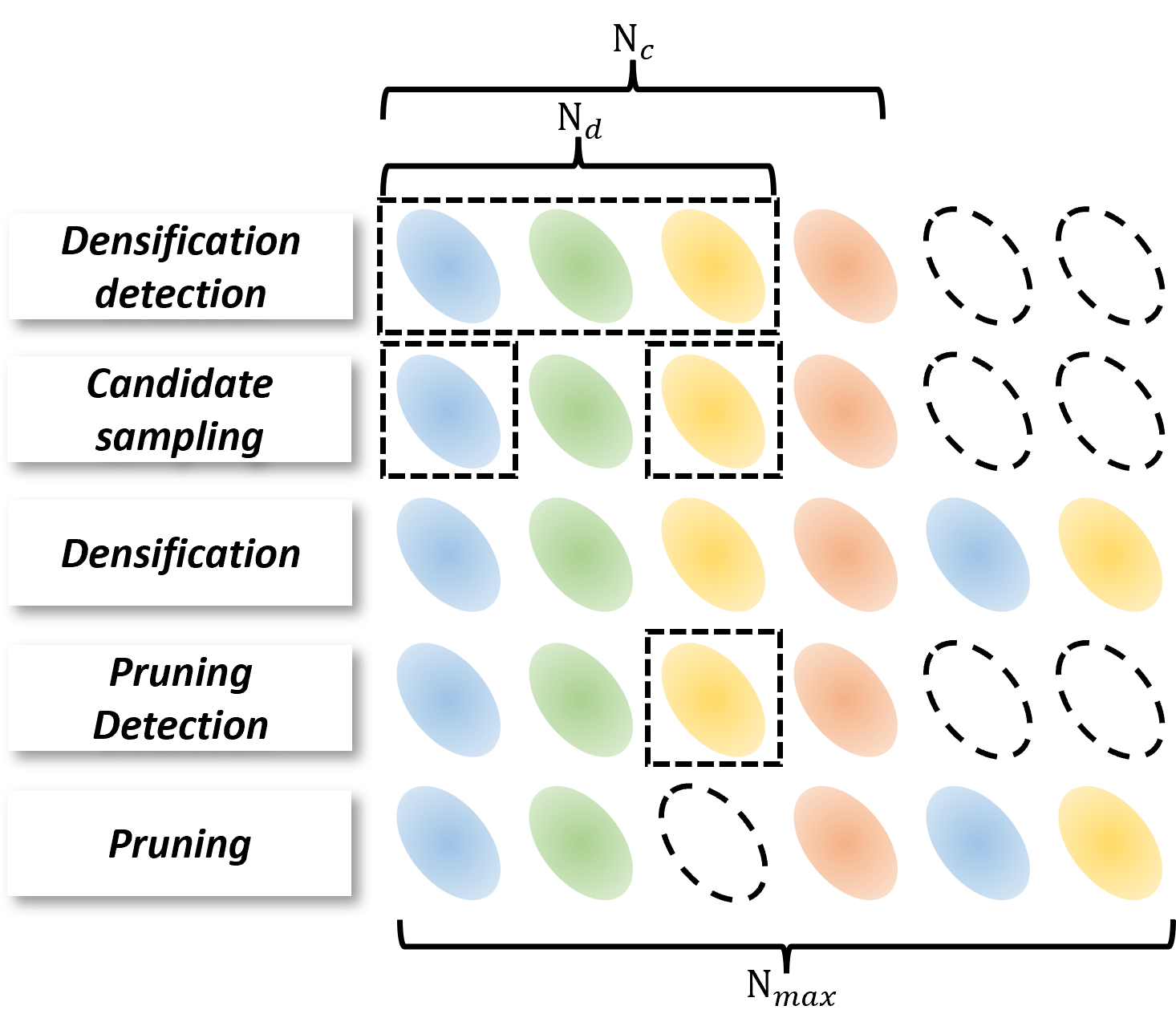
The fitting process encompasses several distinct stages: 1) Densification Detection: Assuming the current iteration includes $N_c$ Gaussians, we identify densification candidates by selecting those with view-space position gradient magnitudes exceeding a predefined threshold $\tau$. We denote the number of candidates as $N_d$. 2) Candidate sampling: To prevent exceeding the predefined maximum of $N_{\text{max}}$ Gaussians, we select $\min{(N_{\text{max}} - N_c, N_d)}$ Gaussians with the largest view-space positional gradients from the candidates for densification. 3) Densification: We modify the densification approach by alternating between cloning and splitting actions into separate steps. 4) Pruning Detection and Pruning: We identify and remove the Gaussians with $\alpha$ less than a small threshold $\epsilon$. After completing the fitting process, we pad Gaussians with $\alpha=0$ to reach the target count of $N_{\text{max}}$ without affecting the rendering results.

Gaussian voxelization via Optimal Transport

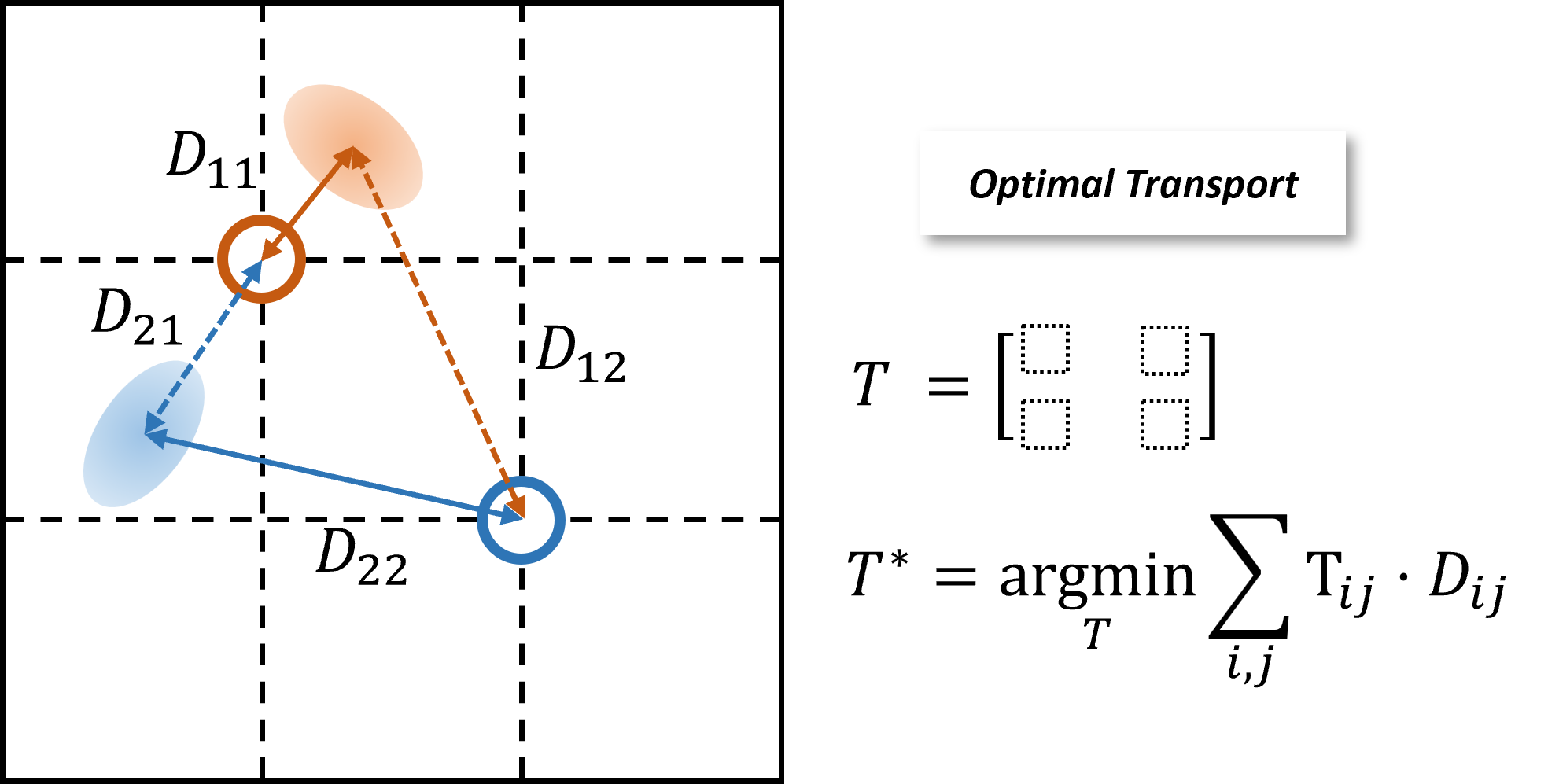
We then employ Optimal Transport to organize the resultant Gaussian into a predetermined voxel grid. Intuitively, we aim to "move" each Gaussian into a voxel grid while maintaining the geometry relations as much as possible. Therefore, we formulate this into an Optimal Transport Problem between the Gaussians' spatial positions and the centers of voxel grid.

Demo Video

BibTeX

@misc{zhang2024gaussiancube,
      title={GaussianCube: Structuring Gaussian Splatting using Optimal Transport for 3D Generative Modeling}, 
      author={Bowen Zhang and Yiji Cheng and Jiaolong Yang and Chunyu Wang and Feng Zhao and Yansong Tang and Dong Chen and Baining Guo},
      year={2024},
      eprint={2403.19655},
      archivePrefix={arXiv},
      primaryClass={cs.CV}
  }